The Wave Function Collapse (WFC) Algorithm

Sources

Here is a blog post from 2018 explaining the principles behind the algorithm.

There is a popular implementation written in C++ for which we'll run through an example.

Analysis

Before we can trace through an example of the values at runtime, one must understand the data structures that we're going to be tracking. The sections below aim to explain that.

tilingwfc.hpp

• The "TilingWFC" class contains a list of Tiles (a one-dimensional structure, oddly enough) and an underlying "WFC" object that does the bulk of the processing.
• One could either start here and zoom in, or start with the lower-level building blocks and build up an understanding from the foundation. But either way, you'll end up looking at the following class, the WFC class — the epicenter of WFC computations.

wfc.hpp

This very low-level intermediate-level class lies just above the 2d-array implementation! It contains just a few key components:

• a "frequency distribution" which is a list of percentages, one for each distinct pattern that can show up in the overall image. This is a list of frequencies whose summation presumably must be equal to 1.
• a "Wave" (an inner class defined below); and
• a "Propagator" (a very cryptic class).

wave.hpp

This class contains:

• a fair amount of "duplicated" properties from the WFC class, like a patterns_frequencies list and the unsigned number storing the number of distinct patterns; but also
• plogp_patterns_frequencies, which is a so-called "precomputation" of p * log(p). I do not fully understand this yet but presumably it helps determine where new tiles are placed while ensuring their overall frequency is as desired;
• data, a two-dimensional array structure, which presumably helps keep track of whether a pattern CAN or CANNOT be placed in a particular location. It contains a 0 if a pattern cannot be placed in a given cell index.

propagator.hpp

Remarkably, this class contains a forward-declaration of the Wave class! But it also contains nitty-gritty data structures like:

• a vector containing 3-tuples (i.e., one element of the vector has the form (y, x, pattern)) — linked to whether wave.data[y + width*x] is set to false (0);
• Array3D<std::array<int, 4>> compatible, a 4-dimensional array containing integers. This bulky structure serves as a way to query HOW MANY patterns are compatible with the given choice of a pattern at (y, x) in the overall tile array. Although this structure is challenging to visualize, this is a case where the documentation does a good job describing it:

le.get(y, x, pattern)[direction] contains the number of patterns present in the wave that can be placed in the cell next to (y,x) in the opposite direction of direction without being in contradiction with pattern placed in (y,x). If wave.get(y, x, pattern) is set to false, then compatible.get(y, x, pattern) has every element negative or null

• a fancy Constructor with an initializer list, but I am getting ahead of myself.

Let's trace through the code using an example. Suppose we have a total of 5 distinct patterns (nb_patterns).

Well, shoot, that means I have to write a full configuration for the rules that dictate which patterns can be placed next to which other patterns.

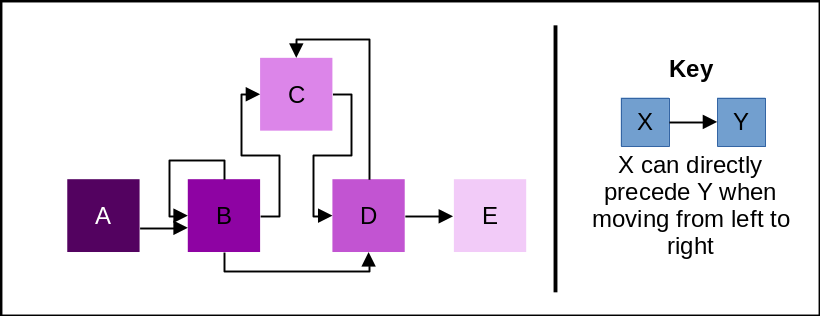
Suppose the ruleset looks something like:

• A can be placed to the left of B
• B can be placed to the left of B
• B can be placed to the left of C
• B can be placed to the left of D
• C can be placed to the left of D
• D can be placed to the left of C
• D can be placed to the left of E

You can treat each letter as representing a unique color or type, or shape, or however you want to envision it. And I guess I need some frequencies for these letters, eh?

Let's use this: {'A': 0.05, 'B':0.5, 'C':0.15, 'D':0.25, 'E':0.05}

Notice that, under this ruleset, the only symbol that can be repeated in a contiguous chunk is "B." No wonder it has the highest frequency!

Now that that's out of the way, how does an iteration of our algorithm look? Let's step through it.

init_compatible()

This is one of only three functions defined on the Propagator, and it is the only one called in the body of the Constructor. It does what it sounds like — populates the compatible private instance variable (see above).

It will be interesting to see where and how this variable gets updated every time a new choice is made.

propagate()

So, already, in the first eight lines of the Propagator::propagate() function, we see the following:

// The cell and pattern that has been set to false.
unsigned y1, x1, pattern;
std::tie(y1, x1, pattern) = propagating.back();

I am reminded of a 2012 Jontron episode where he says, "So immediately he's doing this annoying s***. Like, immediately, he's doing this."

Why do I react so sharply? Well, because I went to a nonsensical university, they didn't offer courses in C++, or at least, not for my major programs. So I am left wondering, how the hell is it possible to use a constructor invocation on the left-hand side of an apparent assignment? I understand that the assignment operator doesn't always mean what you think it means in C++, but this goes a step further. It doesn't even assign a variable name to the result of the tie!

If you are confused by this, then you're not alone. However, the key to understanding is that the tie function, from <tuple>, returns a tuple "containing lvalue references."

So we extract the final triplet (y_ind, x_ind, letter) and save the values into our lvalue references y1, x1, and pattern.